בניגוד למה שמאמינים רבים חושבים בטעות, סדר ומורכבות אינם בהכרח מעידים על תכנון תבוני, או על דבר שנוצר ע"י ישות אינטיליגנטית.
סדר ומורכבות יכולים להיווצר בשתי דרכים עיקריות:


(סדר ומורכבות יכולים להיווצר גם ע"י בעלי חיים. למשל חלת דבש שדבורים מייצרות בכוורת שלהן היא מאוד מסודרת, וקן של טרמיטים מאוד מורכב)

שינויים שמצטברים לאורך זמן:
כפי שתיכף נראה, סדר ומורכבות (ואפילו מורכבות גדולה מאוד) יכולים להיווצר באופן טבעי וללא יד מכוונת, למשל כתוצאה מתהליך אשר חוזר על עצמו שוב ושוב פעמים רבות, בכל פעם על תוצאתו הקודמת.
לתהליך מסוג זה קוראים תהליך רקורסיבי (תהליך שחוזר על עצמו) כשבכל מחזור רמת המורכבות הולכת ועולה, והתוצר נהיה יותר ויותר מורכב.
דברים מורכבים יכולים להיווצר באופן הדרגתי, ע"י סדרה של צעדים פשוטים אשר חוזרים על עצמם שוב ושוב פעמים רבות. כל שלב פועל על מה שכבר נוצר בשלבים הקודמים, ומוסיף עליו מורכבות נוספת.
האבולוציה כדוגמא:
גם האבולוציה היא תהליך רקורסיבי, בו כל דור מקבל בתורשה את תכונותיו של הדור הקודם, משתנה מעט (כתוצאה ממוטציות ותהליך של ברירה טבעית) מעביר את תכונותיו הלאה לדור הבא, ושוב התהליך חוזר על עצמו.
לכן זה לא מפליא בכלל שלאחר מיליארדי שנות אבולוציה, ומאות מיליוני דורות, קיבלנו בעלי חיים בעלי מורכבות גדולה כל כך כפי שאנו רואים כיום.
זה בדיוק מה שאנחנו מצפים לראות מתהליך רקורסיבי, החוזר על עצמו שוב ושוב במשך תקופה כל כך ארוכה, פעמים כה רבות, ולא רק במקום אחד, אלא באינספור מקומות במקביל על פני כדור הארץ.
לא רק שמורכבות אינה מעידה באופן אוטומטי על תכנון תבוני, אלא שהרבה פעמים דווקא פשטות היא זו שמעידה על תכנון תבוני ויעילות.









אם מורכבות מחייבת תכנון תבוני, אי אפשר להתחמק מהשאלה:
מי יצר, או מי ברא את אלוהים?
זה לא משנה אם אלוהים חומרי או לא חומרי, בתוך הזמן או מחוץ לזמן, כדי שיהיו לו כל התכונות המופלאות שמיוחסות אליו, הוא חייב להיות פי מיליארדים יותר מורכב מכל מה שאנחנו מכירים בעולם הזה.
כלומר לפי אותו היגיון וקו מחשבה, גם לאלוהים חייב להיות בורא.
לא יעזרו כל התירוצים.

אולי אחת הדוגמאות הכי מוכרות, לסדר שנוצר מעצמו ללא מסדר:
נערבב היטב שמן ומים בכוס, עד שיווצר בלגאן, נניח בשקט על השולחן ונמתין. תוך מספר דקות יווצר לנו בכוס סדר מופתי, למטה תמצא שכבה אחידה של מים, ומעליה שכבה אחידה של שמן.
כיצד זה קרה?
כוח המשיכה של כדור הארץ, והמסות השונות של מולקולות המים והשמן, יצרו יחד הפרדה לשתי שכבות נפרדות:
מולקולות המים שהן כבדות יותר ממולקולות השמן, נמשכו בחוזקה כלפי מטה, תוך שהן דוחפות את מולקולות השמן כלפי מעלה שיפנו להן מקום. כמו בריונים שנדחפים בתור לסרט ודוחפים את כולם לאחור.
זוהי דוגמה פשוטה, לכוחות פיזיקליים אשר יוצרים סדר בבלגאן.
והנה דוגמה נוספת לסדר, מורכבות ואפילו יופי הנוצרים באופן טבעי.








פתיתי השלג המרהיבים והסימטרים האלו נוצרו בצורה טבעית, כתוצאה מהתגבשות אדי מים קפואים בגובה העננים.
נקודה למחשבה:
אם פתיתי שלג מורכבים ויפים כל כך נוצרו בתוך מספר דקות, שערו בנפשכם איזו מורכבות יכולה להיווצר במשך מיליארדי שנים... תשובה לטענה הדתית שלפיה גופנו "מורכב מדי" ולכן לא יכל להיווצר בדרך טבעית של אבולוציה.

כיצד התבנית הזו נוצרה?
התבנית הסימטרית, המורכבת והיפה הזאת נוצרה כתוצאה מחזרה (שוב ושוב אלפי פעמים) על כלל אחד פשוט:
בכל מחזור, התוכנה הגרילה באופן אקראי את אחד משלושת הקודקודים של המשולש הגדול, וציירה פיקסל לבן בדיוק באמצע, בין הנקודה הנוכחית (הנקודה האחרונה שציירנו) ובין הקודקוד שהוגרל.
(התוכנה מתחילה תמיד בקודקוד העליון כנקודת התחלה)
כמה מכם יכלו לנחש כי כלל כל כך פשוט, ייצור דבר כל כך מורכב ומסודר?
אין כאן שום חוקי פיזיקה, ושום כוחות פיזיקליים, רק מתמטיקה טהורה! איפה אלוהים מסתתר כאן? איך הוא קשור לעניין?
פרקטל:
תבנית מסוג זה נקראת פרקטל, זוהי צורה או תבנית אשר חוזרת על עצמה שוב ושוב (לפעמים בווריציות שונות) כאשר מבצעים הגדלה על אזור מסויים בה.
האם אלוהים יצר את המתמטיקה?
אין שום סיבה לתת קרדיט לאלוהים (גם לא לגבי דוגמאות נוספות שנראה בהמשך) ולהניח שהוא "ייצר את המתמטיקה" שאיפשרה למורכבות הזו להיווצר.
מתמטיקה היא דבר אוניברסלי, היא נכונה בכל מקום ובכל זמן. תפוח ועוד תפוח תמיד יהיו יחד שני תפוחים, שלושה ארגזים שבכל אחד מהם 25 כדורי טניס יכילו תמיד סה"כ יחד 75 כדורים.
קשה להאמין כי ייתכן יקום שבו המצב שונה, יקום שבו תפוח ועוד תפוח שווים יחד 5 תפוחים, או כל נושא מתמטי אחר שאינו תואם למתמטיקה שאנחנו מכירים.
על פניו נראה שהמתמטיקה היא הכרח של המציאות, וקיימת תמיד, לכן אין שום צורך "לברוא" או להמציא אותה, אלא רק לחקור ולנסות להבין אותה טוב יותר.

תמונה מקסימה זו מתקבלת, כאשר מבקשים מהמחשב לצבוע כל פיקסל בהתאם למרחקו מכל אחד משלושת הקודקודים.
נקבע בתוכנה, כי ככל שהפיקסל קרוב יותר לקודקוד העליון, כך ערכו של צבע היסוד האדום של הפיקסל עולה, בעוד שהירוק והכחול נחלשים. ככל שהפיקסל קרוב יותר לקודקוד השמאלי התחתון, כך צבעו הירוק מתחזק, והצבע האדום והכחול נחלשים, ודבר דומה לגבי הקודקוד הימני, שמייצג את הצבע הכחול.
כידוע צבעו של כל פיקסל נקבע ע"י שילוב של שלושת צבעי היסוד:
אדום, ירוק, כחול.
דוגמא נוספת למורכבות הנוצרת מתוך פשטות.
הביטו בשלושת התבניות המורכבות הבאות:



הפסקת חשיבה
לפני שתמשיכו לקרוא, האם תוכלו לנחש מה הכלל הפשוט שיצר את כל אחת משלושת התבניות המורכבות, המסודרות והיפות האלה?
ובכן...
התבנית הראשונה:
התבנית הראשונה נוצרה ע"י כלל אחד פשוט ביותר:
גוון האפור של כל פיקסל בתמונה, הוא מספר הטור של אותו פיקסל (ציר x) כפול מספר השורה שלו (ציר y). למשל הפיקסל שנמצא בטור 5, שורה 7, קיבל רמת אפור 35, זאת משום ש 7 כפול 5 הם 35.
התבנית השנייה:
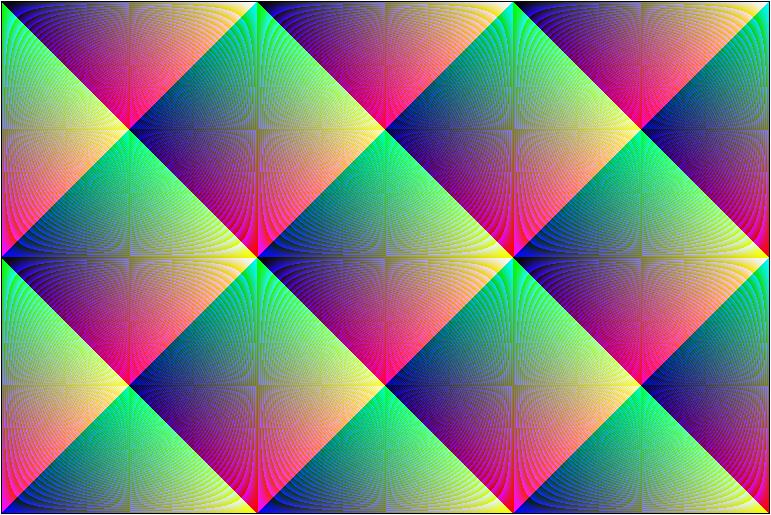
לקבלת התבנית השנייה שונה תו אחד בלבד בקוד. סימן הכפל שונה לסימן חזקה, כך שרמת האפור של כל פיקסל, היא מיקומו בציר x בחזקת מיקומו בציר y.
שינוי זעיר בקוד, ואיזו השפעה דרמטית על התוצאה...
אם נעשה לרגע הקבלה לנושא האבולוציה, גם שם שינוי זעיר בקוד הגנטי של בעל חיים (אפילו של אות אחת) יכול ליצור לעיתים שינוי דרמטי במבנה גופו ובתכונותיו של אותו בעל חיים. שינוי שיכול להזיק, אך לעיתים גם יכול להביא לו תועלת.
התבנית השלישית:
לקבלת התבנית השלישית, שוב שונה תו אחד בלבד בקוד:
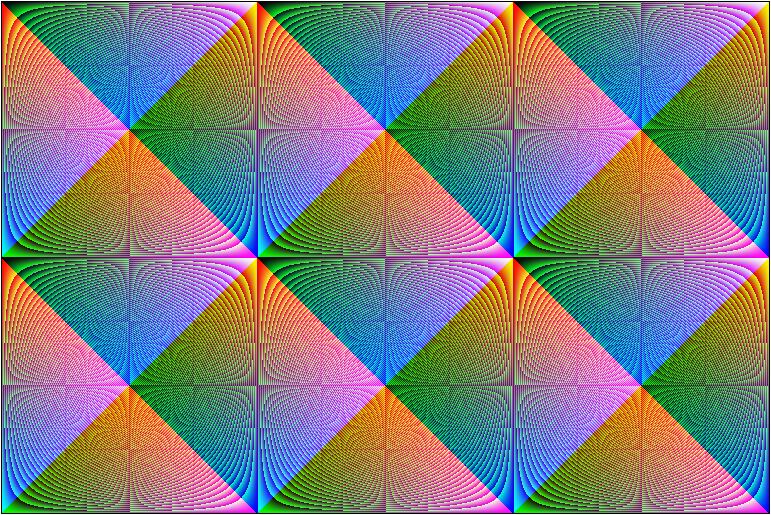
סימן החזקה ^ שונה לסימן %, שאומר למחשב כי רמת האפור של כל פיקסל תהיה שווה לשארית החלוקה של מיקומו בציר x, חלקי מיקומו בציר y.
ראו כיצד כללים כל כך פשוטים יוצרים מורכבות גדולה, סדר וסימטריה, ואפילו אין כאן חזרתיות (רקורסיה) אלא מעבר אחד בודד על כל פיקסל!
הערה צדדית:
צבעו של כל פיקסל בתוכנה נשמר במשתנה מסוג byte היכול לקבל ערכים בתחום של בין 0 ל 255. לכן, בכל פעם שתוצאת הפעולה המתמטית (למשל x כפול y) עולה מעל 255, הערך מתגלגל חזרה לאפס וחוזר חלילה (למשל אם תוצאת פעולת הכפל היא 280, הפיקסל יקבל רמת אפור 25, משום ש 280 פחות 255 הם 25).
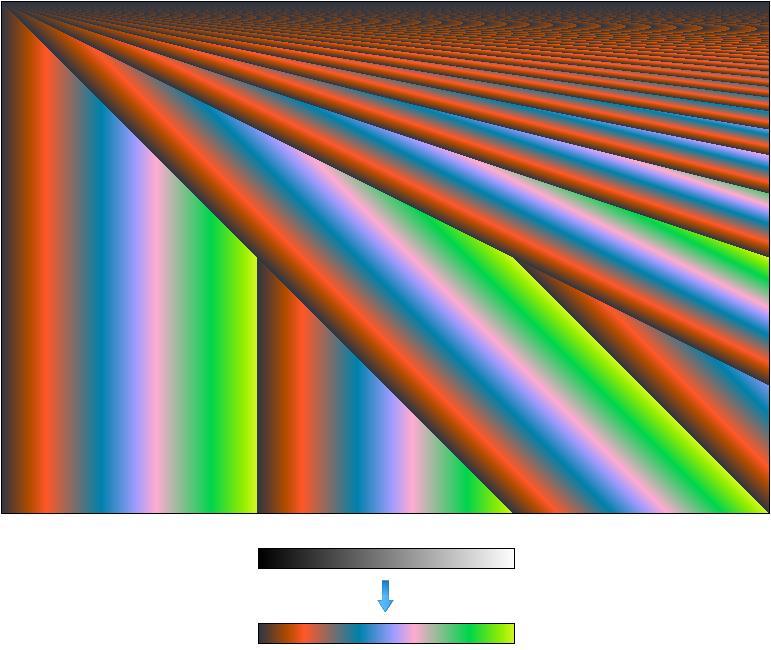
זה מה שמתקבל כאשר ממירים את גווני האפור בתמונה לפאלט צבע אקראי.

דוגמא נוספת, עם פאלט צבע אקראי אחר.



התבניות היפות והצבעוניות האלה התקבלו, לאחר שביקשנו מהמחשב להגריל בתחילת כל הרצה באופן אקראי, האם להשתמש בפעולת חיבור, חיסור, כפל, חזקה או שארית לקביעת ערכם של צבעי היסוד של הפיקסלים (כאמור צבעו של כל פיקסל נקבע ע"י ערבוב של שלושת צבעי היסוד: אדום, ירוק וכחול).

זה מה שמתקבל כשמבקשים מהמחשב "להתפרע" ולבחור באקראי עבור כל צבע יסוד (אדום, כחול, ירוק) של כל פיקסל ופיקסל באיזו פעולה חשבונית להשתמש:
חיבור, חיסור, כפל, חזקה או שארית.

מה זה?
זהו פרקטל מנדלברוט, אחד הפרקטלים הכי מוכרים בעולם הפרקטלים.
הפרקטל קרוי על שמו של בֶנוּאה מנדלבּרוֹט, פרופסור (יהודי-צרפתי-אמריקאי) למתמטיקה שגילה אותו כאשר השתעשע עם הצגה ויזואלית של נוסחאות מתמטיות על מחשב IBM שאליו הייתה לו גישה במסגרת עבודתו.
במבט ראשון הפרקטל עשוי להיראות אולי מעט משעמם, אך עוד רגע נראה כמה יפה, מרהיב ומורכב הוא נראה כשמתחילים לעשות עליו זום...
כיצד הפרקטל הזה נוצר?
הפרקטל נוצר ע"י נוסחה מתמטית קצרה ופשוטה אותה אנו מפעילים בצורה רקורסיבית על כל אחד מהפיקסלים בתמונה (כאשר היא עדיין לבנה וריקה) ועל פי התוצאה שמתקבלת מחליטים באיזה צבע לצבוע אותו.
נבחר פיקסל כלשהו שאותו אנו רוצים לבדוק, ואז:






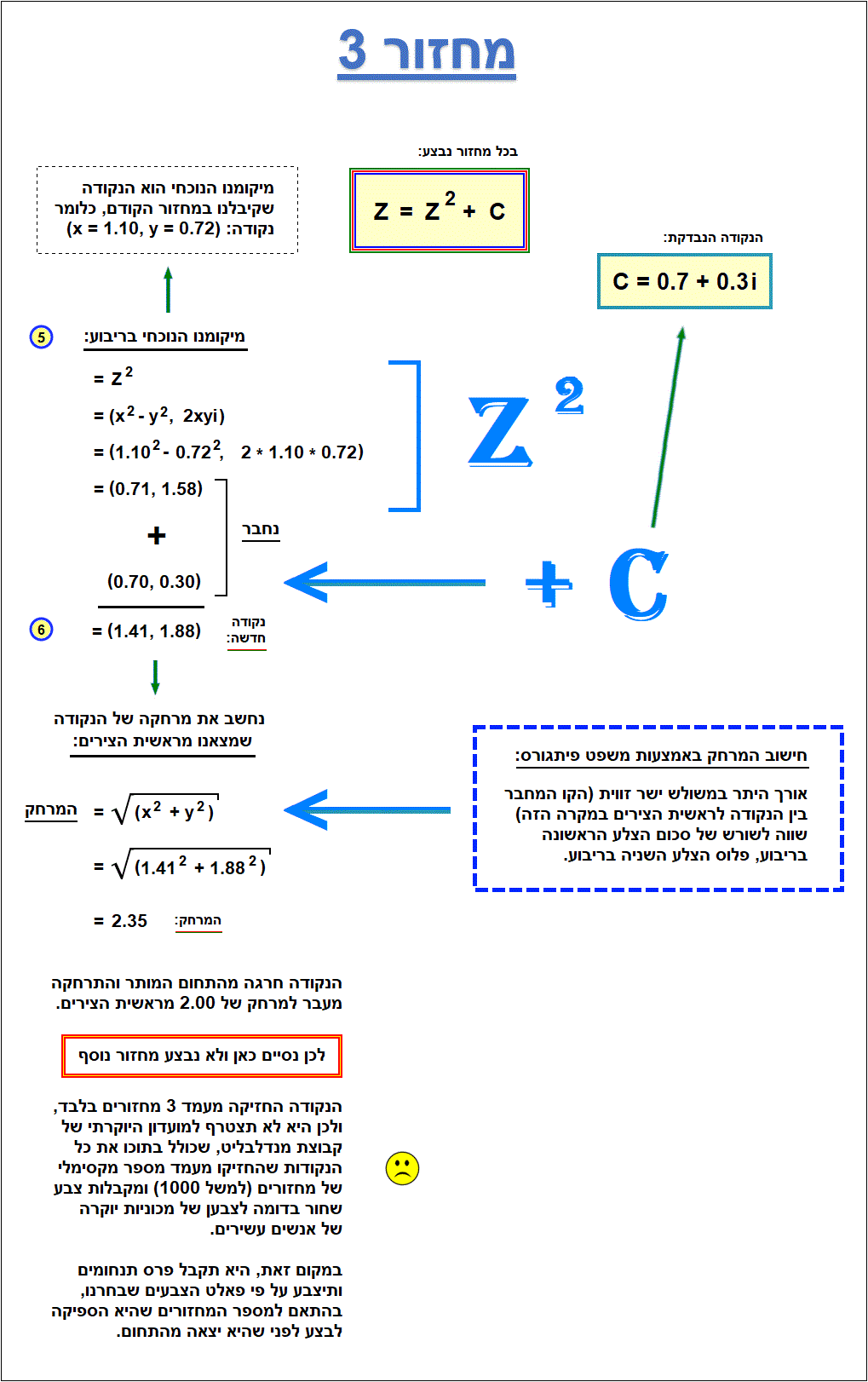
עכשיו, כל מה שנותר לנו לעשות זה לבדוק כמה מחזורים עברו עד שהנקודה "עפה" מחוץ לתחום... אם היא "החזיקה מעמד" מספר רב של מחזורים (למשל 1000 מחזורים ומעלה) אז אנחנו אומרים שהיא שייכת ל"קבוצת מנדלברוט", וצובעים אותה בשחור.
אם היא החזיקה מעמד מספר קטן יותר של מחזורים, אז אנחנו צובעים אותה לפי כל פאלט צבע שמתחשק לנו, בהתאם למספר המחזורים שהיא הספיקה לעשות לפני שהיא יצאה מחוץ לתחום.
למשל, אם היא החזיקה מעמד מספר קטן של מחזורים, אנחנו צובעים אותה בצהוב. אם החזיקה מעמד קצת יותר, צובעים אותה בכתום, החזיקה יותר? צובעים אותה בצבע אדמדם, החזיקה יותר? צובעים בכחול... ואז בתכלת... ולבן.
כאמור הצבעים כאן הם רק לשם המחשה וניתן לבחור כל פאלט צבע שרוצים.
מספרים מרוכבים
לא ניכנס לעניין יותר מדי לעומק, את זה מומלץ לעשות דרך דף הקישורים והסרטונים המצויינים שמופיעים בו אשר מסבירים את הנושא בפירוט.
נאמר רק בקצרה כי כל נקודה (כלומר כל פיקסל) מיוצגת ע"י:
X + Yi
כאשר X הוא מספר ממשי, Yi הוא מספר מדומה, ושניהם יחד נקראים "מספר מרוכב".
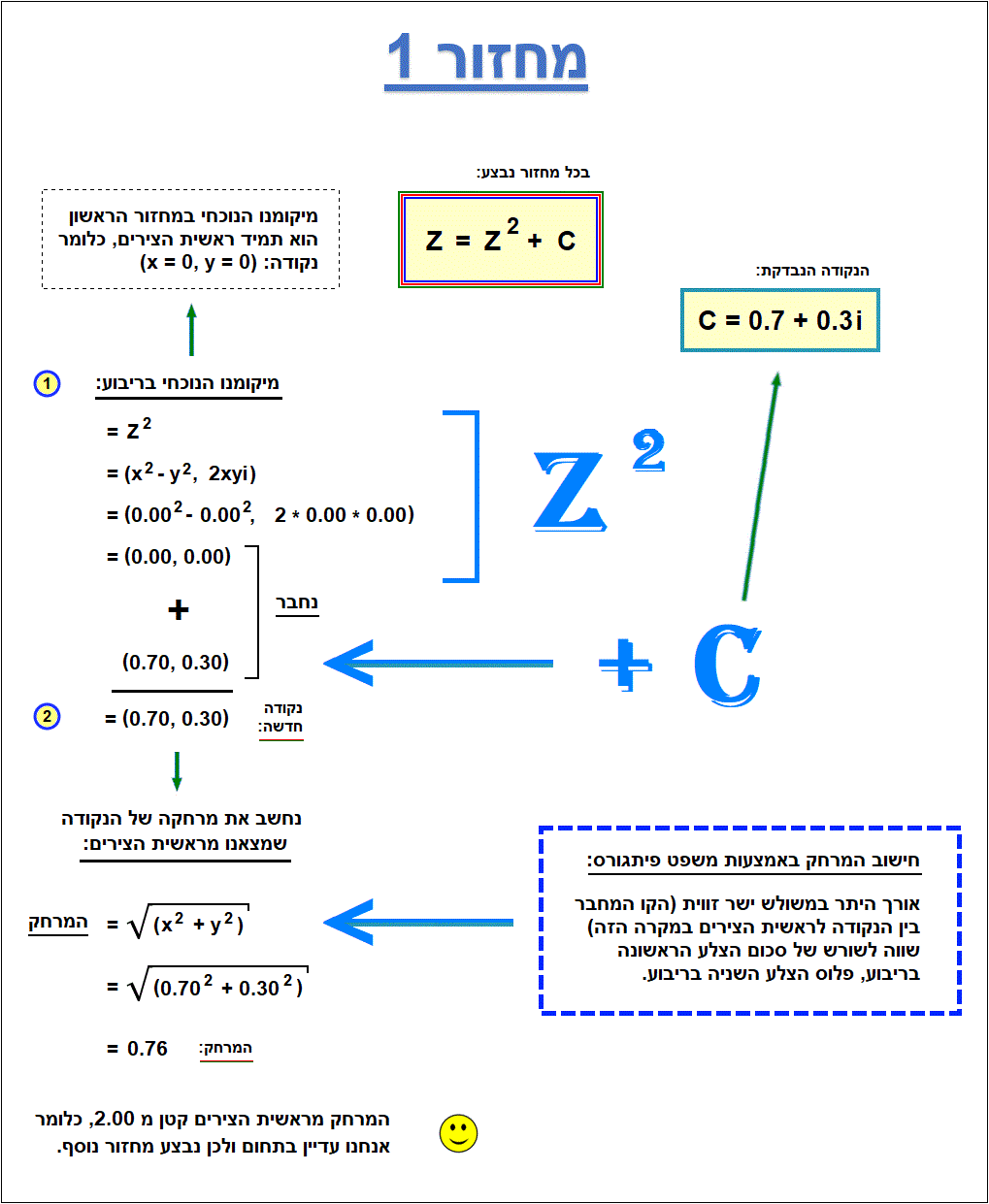
המתמטיקה כאן פשוטה מאוד, למשל כאשר בסעיף הראשון (של המחזורים) אנו מעלים את מיקומנו הנוכחי בריבוע, אנו בעצם מחשבים כמה זה:
(X + Yi) בחזקת 2.
ההבדל היחיד לעומת מתמטיקה רגילה הוא שכאשר אנחנו פותחים את הסוגריים, ומכפילים את Yi בעצמו, הסימן של התוצאה מתהפך (תוצאה חיובית הופכת לשלילית, ולהיפך) והאות i שציינה כי מדובר במספר מדומה נעלמת.
כלומר התוצאה הופכת למספר ממשי (לא מדומה) בעל סימן הפוך, זאת משום שעל פי ההגדרה i בריבוע שווה למינוס 1.
במחשבה שנייה...
במחשבה שנייה, אולי בכל זאת ניכנס קצת לעומקם של הדברים, אך מי שיעקוב יראה כי הדבר לא כל כך מסובך, ואפילו דיי מעניין.
מי שלא מעוניין בהסברים, מוזמן לדלג לתמונות היפות שנמצאות מיד בהמשך...

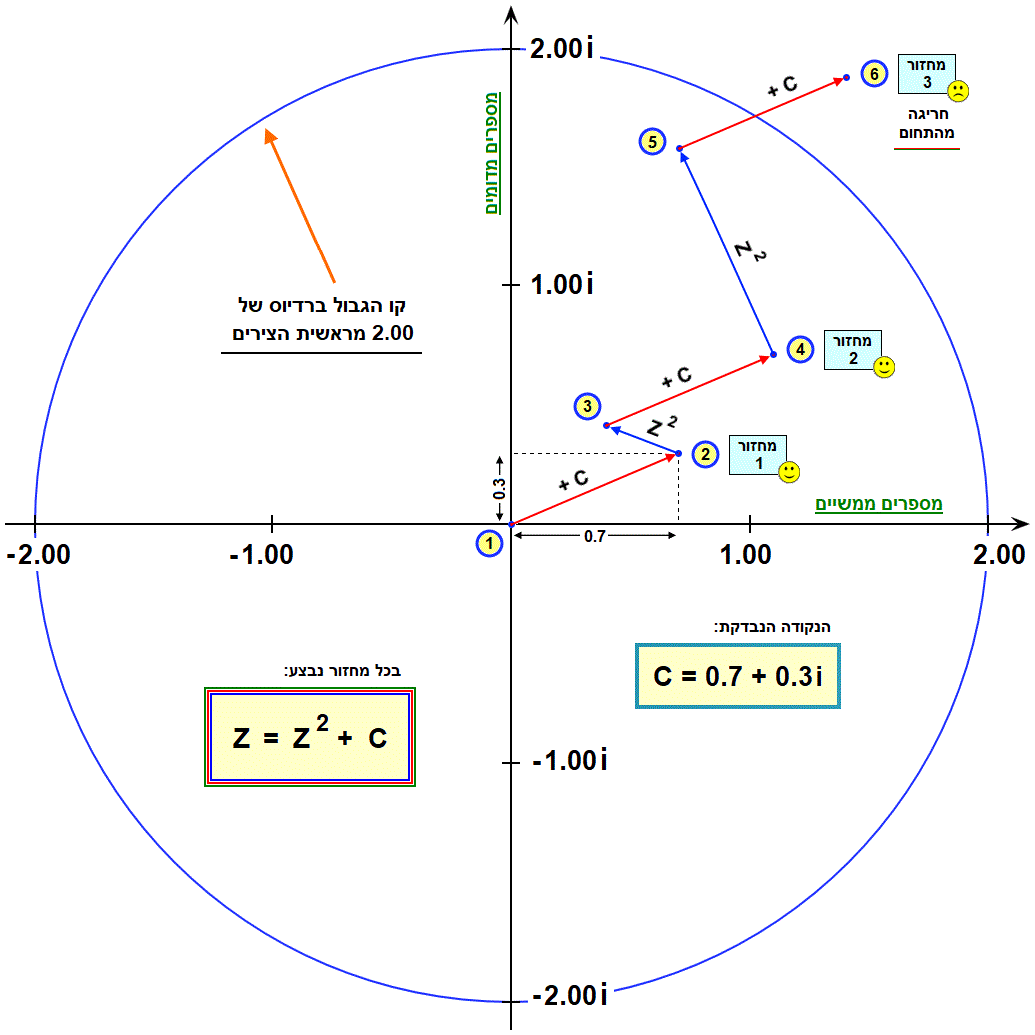
הסבר לאיור:
נבחר נקודה כלשהי (x=0.7, y=0.3) ונבדוק באיזה צבע עלינו לצבוע אותה...
בדוגמא זו מתבצעים 3 מחזורים, ובכל אחד מהם שני שלבים פשוטים:


שני שלבים פשוטים, שחוזרים על עצמם שוב ושוב בצורה רקורסיבית (בכל פעם על תוצאתם הקודמת) ויוצרים את המורכבות המופלאה שנראה עוד מעט...
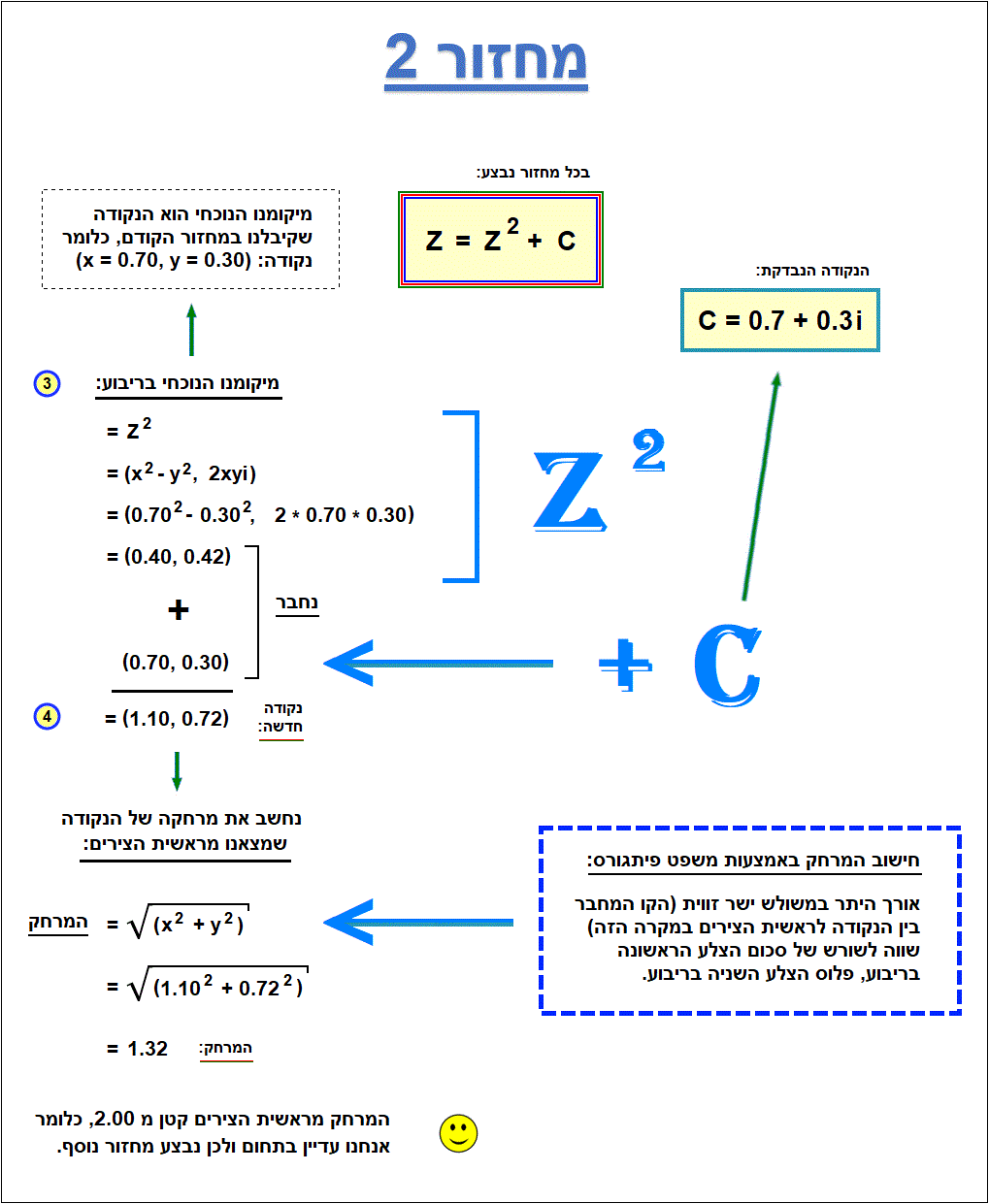
בסיום המחזור הראשון (נקודות 1, 2) אנחנו עדיין בתחום (בתוך העיגול הכחול שמסמן את קו הגבול) ולכן נבצע מחזור נוסף. גם בסיום המחזור השני (נקודות 3, 4) אנחנו עדיין בתחום ולכן נבצע עוד מחזור.
בסיום המחזור השלישי (נקודות 5, 6) אנחנו כבר חוצים את התחום המותר, ולכן נסיים וניגש לצבוע את הנקודה (או הפיקסל, איך שתרצו) בהתאם למספר המחזורים שהיא הספיקה לעשות.
להלן פירוט אופן החישוב עבור כל שלב באיור:
נחזור לחלק האומנותי
אחרי שהבנו כיצד זה עובד, נראה כמה דוגמאות מרהיבות של פרקטל זה כפי שהוא נראה בהגדלה, כלומר כאשר עושים עליו זום.
תחילה נראה אותו בדו מימד, ולאחר מכן בתלת מימד.





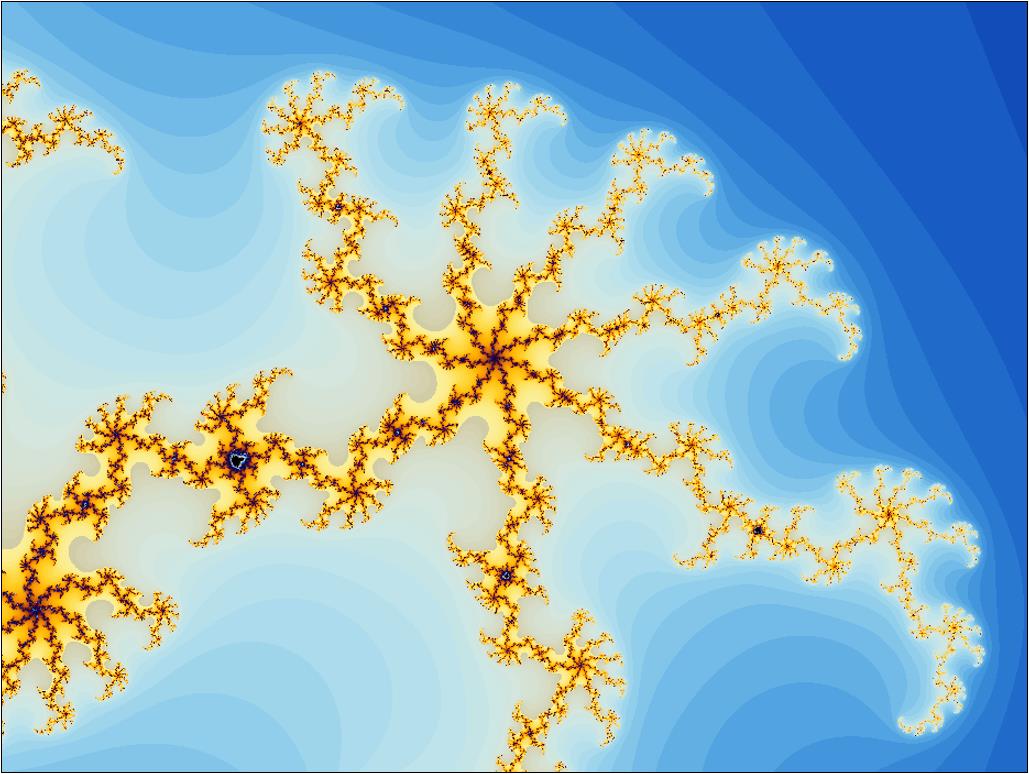
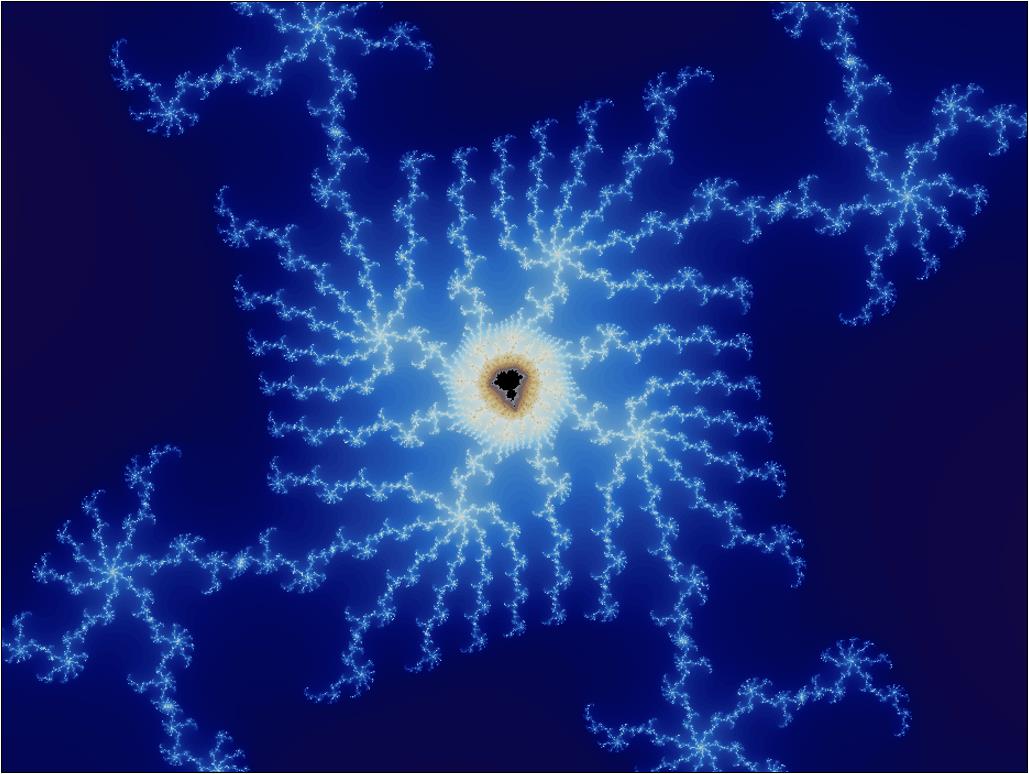
נ.ב - שתי התמונות האחרונות נוצרו ע"י אפליקציה שמיד יינתן קישור אליה.
עבודת אמן?
בואו נודה באמת, מי שאינו מכיר את הפרקטל ויראה את התמונות האלו בפעם הראשונה יהיה בטוח כי מדובר בעבודתו של אמן מאוד מוכשר...
מי היה מאמין שנוסחה מתמטית כל כך קצרה ופשוטה אשר חוזרת על עצמה שוב ושוב בצורה רקורסיבית (בכל פעם על תוצאתה הקודמת) יכולה ליצור מבנים כל כך מרהיבים, מורכבים ויפים?
אבל זו עובדה, הציורים המקסימים והמורכבים האלה נוצרו באופן טבעי, ללא שום תכנון או יד מכוונת. התכנת שכתב את התוכנה אשר מציגה את הפרקטל, בסך הכל חשף עבורנו בצורה ויזואלית את המתמטיקה שתמיד הייתה שם.
זאת בדומה להמצאת המיקרוסקופ, שאיפשר לנו לראות עולם שלם של חיידקים ויצורים מיקרוסקופיים שהיו כל הזמן מתחת לאף שלנו, אך עכשיו בזכות המיקרוסקופ אנחנו יכולים סוף סוף לראות אותם לנגד עינינו.
חתימת ידו של אלוהים?
רבים רואים בפרקטל מנדלברוט את "חתימת ידו של אלוהים", או את טביעת האצבע שלו. אך האם הדבר באמת נכון?
התשובה היא שלילית.
פרקטל מנדלברוט בסך הכל מוכיח כי חוקים פשוטים, יכולים ליצור מורכבות גדולה ביותר וסדר. מה שיכול היה להוכיח כי פרקטל זה הוא פרי יצירתו של אלוהים, היה למשל אם היינו מבצעים זום (כלומר הגדלה) על אזור מסויים בפרקטל, ופתאום היה מתגלה לפנינו כיתוב ברור שאומר:
"אני יהוה בורא האדם והעולם, אלוהי התורה שהוציא את עם ישראל מארץ מצרים, ופרקטל זה הוא פרי תכנוני ויצירתי".
דבר כזה מעולם לא התגלה, וכנראה שגם לא יתגלה.
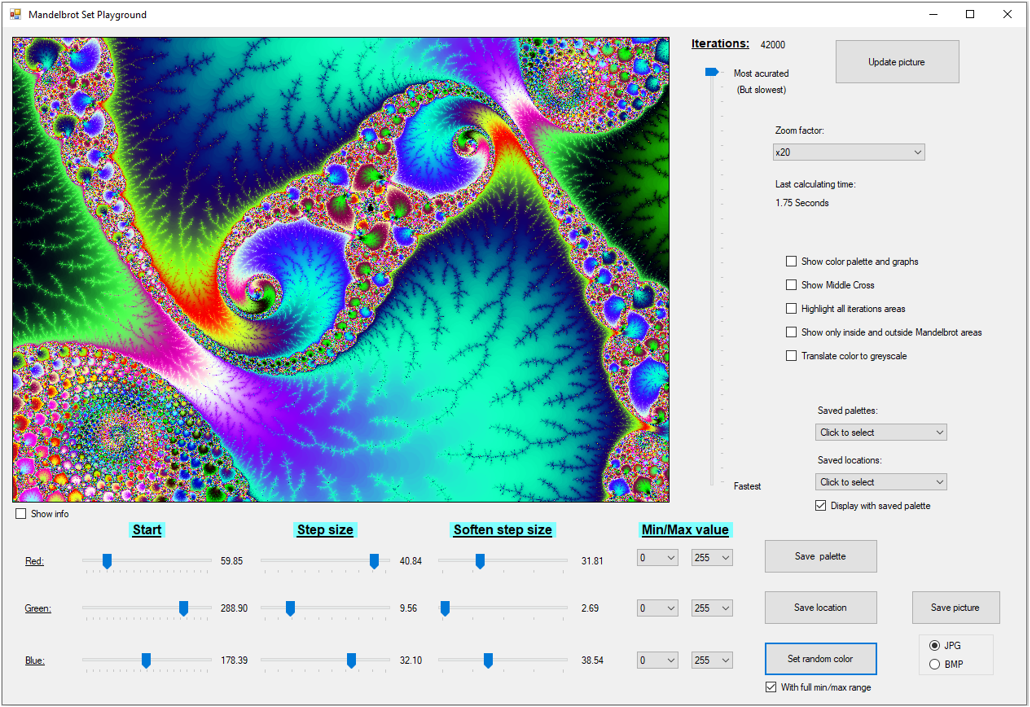
בדף זה תוכלו להוריד אפליקציה חינמית, פשוטה וידידותית (פרי פיתוח עצמי) להצגת פרקטל מנדלברוט. האפליקציה מאפשרת לבצע זום על כל נקודה בפרקטל, להציגו בעזרת פאלט צבע גמיש הניתן לשינוי והתאמה לתמונה המוצגת, ואופציות מעניינות נוספות אותן ניתן לראות בצילום המסך.
(הקוד עצמו גם כן זמין להורדה)
מצאתם תמונות יפות? שתפו!
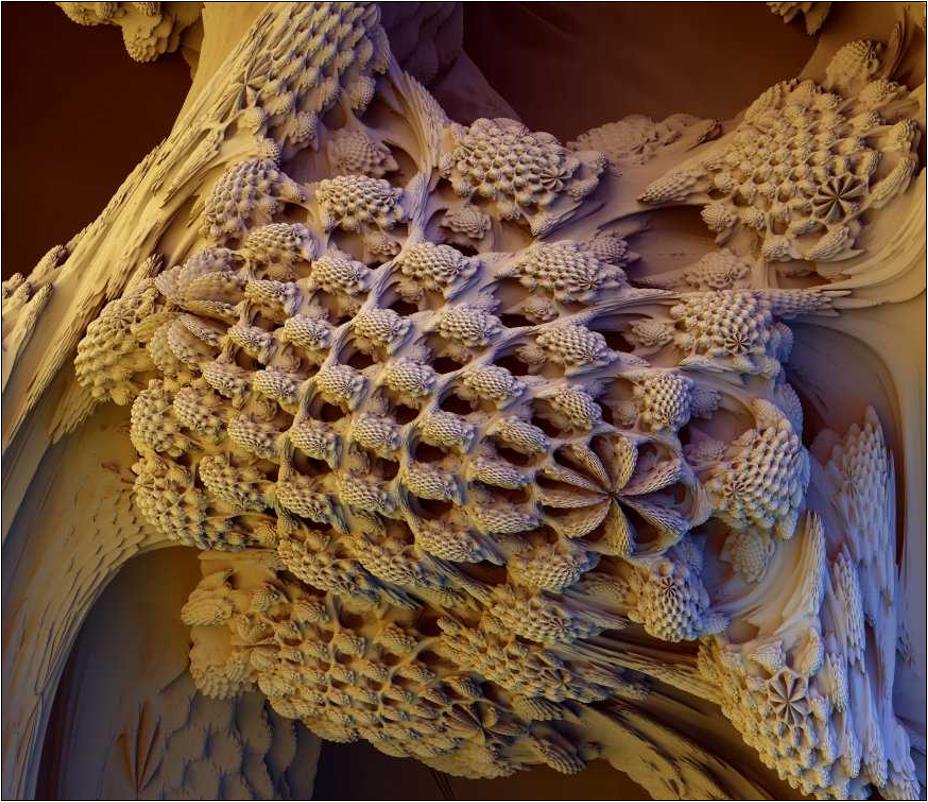


כן, כך נראה פרקטל מנדלברוט בתלת מימד, הוא פשוט לא מפסיק להפתיע...
כאילו שבדו מימד הוא לא נראה מספיק יפה ומורכב. להסבר מפורט על האופן שבו נוצרה הגרסה התלת מימדית של פרקטל זה, נא לבדוק את דף הקישורים.
(אם בעל האתר לא ישכח לשים את הקישור)


סדר יכול להיווצר גם בתוך אקראיות מוחלטת.
בתמונות אפשר לראות אזורי סדר שנמצאו בהגרלה אקראית לחלוטין של 374 מיליון ספרות, כל אחת בתחום של בין 0 ל 9.
במרכז על רקע צהוב, מסומן אזור סדר מרכזי שהתוכנה זיהתה באופן אוטומטי לאחר ביצוע ההגרלה, ומסביב מסומנים אזורי סדר קטנים יותר שנמצאו בסריקה ידנית של המטריצה במבט מהיר בעין.
בהגרלה ספציפית זו, שהינה הגרלה מייצגת (הגרלות נוספות שבוצעו לפני ואחרי נתנו תוצאות דומות מאוד) התוכנה מצאה את אזורי הסדר הבאים:
8, 7, 6, 5, 4, 3, 2, 1: סדרה זו נמצאה פעמיים.
1, 2, 3, 4, 5, 6, 7, 8: סדרה זו נמצאה 3 פעמים.
4, 4, 3, 3, 2, 2, 1, 1: סדרה זו נמצאה 5 פעמים.
6, 2, 9, 5, 1, 4, 1, 3: הספרות הראשונות של פאי, סדרה זו נמצאה פעמיים.
1, 8, 5, 3, 2, 1, 1, 0: תחילתה של סדרת פיבונאצ'י, סדרה זו נמצאה 4 פעמים.
הסטטיסטיקה מבטיחה סדר:
הסטטיסטיקה מבטיחה לנו שבמרחב מספיק גדול של בלגאן, בהכרח יווצרו לנו גם כמה אזורים קטנים (או "איים") של סדר.
דווקא אם לא יווצרו אזורים קטנים של סדר בתוך מרחב מבולגן גדול, זה יהיה הדבר אשר אמור להפתיע אותנו. דווקא מצב כזה ירמוז על אפשרות של התערבות חיצונית, שדאגה למנוע היווצרות של אזורי סדר קטנים בתוך המרחב המבולגן.
הסדר שקיים על כדור הארץ:
אחרי שהבנו את זה, כבר יותר קל להבין כיצד במרחב העצום של היקום בו אנו חיים, המכיל מאות מיליארדי גלקסיות, שכל אחת מכילה מאות מיליארדי שמשות, שסביב כל אחת סובבים כוכבי לכת (פלנטות) יכולים להיווצר כיסים זעירים של סדר כמו זה שקיים על כדור הארץ, שהוא רק גרגר אבק ביקום העצום סביבנו...