על מה מדובר?

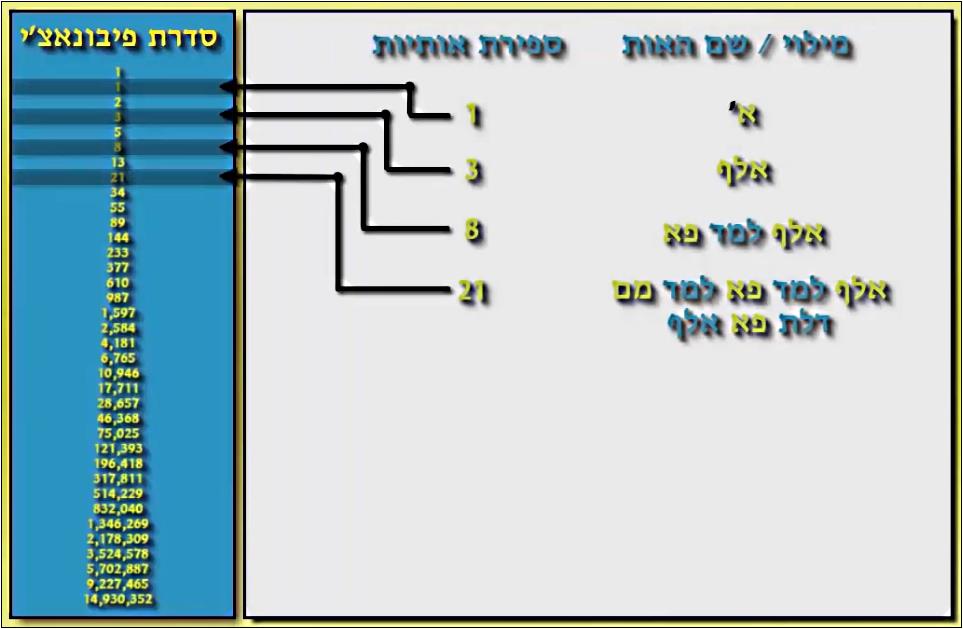
בסרטון שניתן לראות כאן, מראה יוצר הסרטון כי ישנן אותיות באלפבית העברי, שאם נכתוב את השם המלא שלהן, ונמשיך לפרט את שמה המלא של כל אות, ונחזור על כך שוב ושוב פעמים רבות, נראה כי מספר האותיות הנוצרות בכל שלב תואם בצורה מושלמת לסדרת פיבונאצ'י במיקומים הזוגיים או האי זוגיים!

למשל, אם ניקח את האות א' (אות אחת) ונכתוב את שמה המלא, נקבל:

אלף (סה"כ 3 אותיות).

נכתוב שוב כל אות (במילה "אלף") בשמה המלא, ונקבל:

אלף, למד, פא (סה"כ 8 אותיות).

נמשיך כך שוב ושוב כמה פעמים שנרצה... ונקבל את סדרת פיבונאצ'י בכל המיקומים האי זוגיים!

מה היא סדרת פיבונאצ'י?

סדרת פיבונאצ'י היא סדרת מספרים, שבה כל ערך הינו סכום של שני המספרים שקדמו לו. הסדרה מתחילה בספרות 0, 1 שהן קבועות, והחל מהערך השלישי (שהוא 1) כל ערך הוא כאמור סכום של שני הערכים שהיו לפניו.

הנה הערכים הראשונים של הסדרה:

0, 1, 1, 2, 3, 5, 8, 13, 21....

למשל הערך 5, הוא סכום של שני הערכים שקדמו לו: 2 ו 3.

(מעניין אגב, שלפי הסרטון הסדרה מתחילה כביכול בערך 1, כשבפועל היא מתחילה תמיד ב 0... ואפשר לבדוק זאת בכל דף אינטרנט שעוסק בנושא)

ממש פלא פלאים...

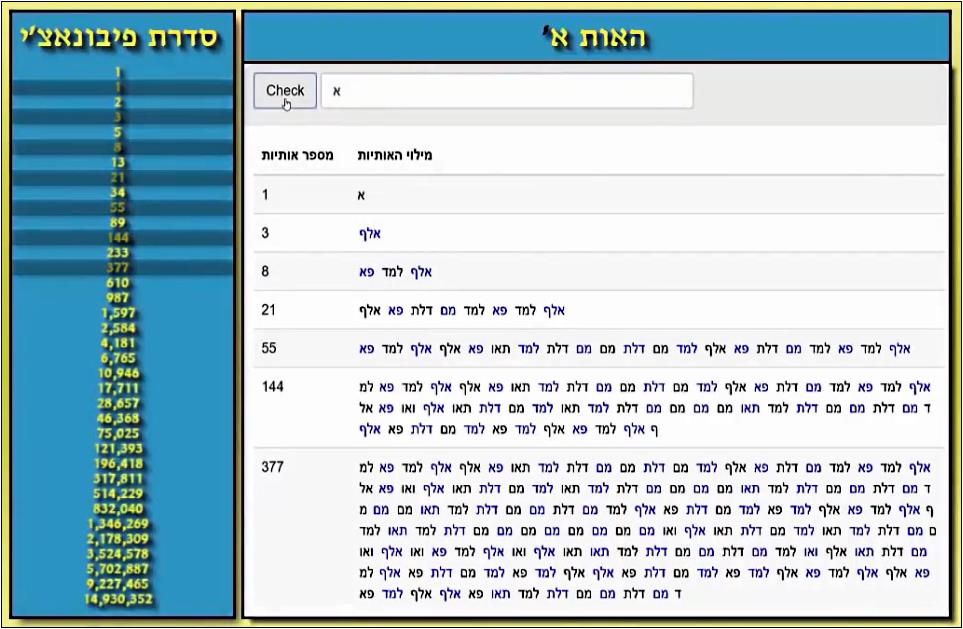
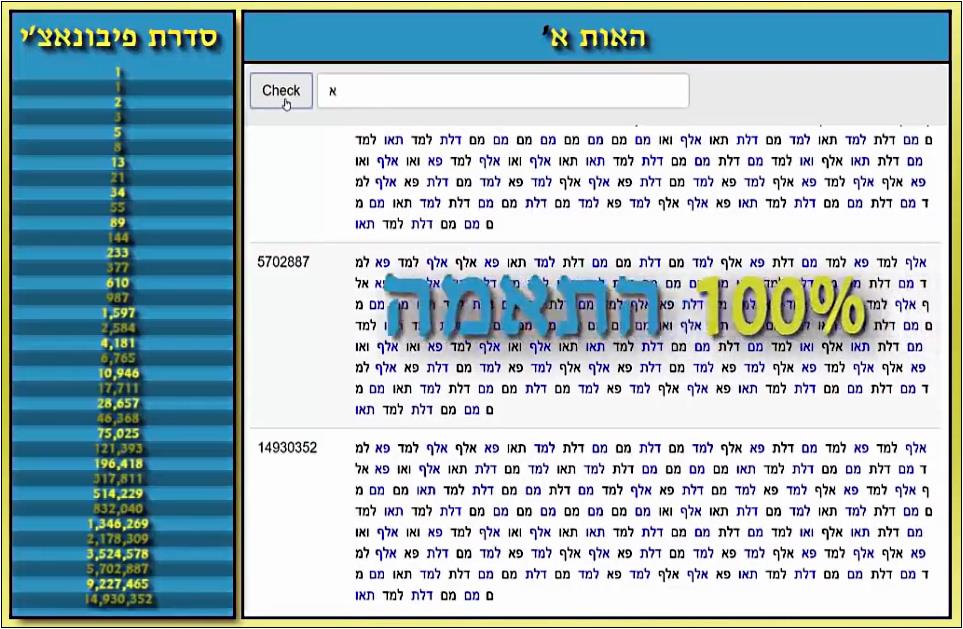
הפלא מתרחש רק כאשר משתמשים באיות ספציפי של האלפבית העברי, איות שלדברי יוצר הסרטון מופיע בספרי קודש רבים...

צילומי מסך מתוך הסרטון (לא כולל ההדגשות והתוספות).

שימו לב שישנן 3 אלטרנטיביות אפשריות לארבעת האותיות במילוי, מי שבחר את האלפבית שיוצר את סדרת פיבונאצ'י החליט להשתמש דווקא באופצייה הראשונה, וכרגיל מספקים לבחירה הזו הסברים ותירוצים בדיעבד...

אם האופצייה השנייה או השלישית היו נותנות את סדרת פיבונאצ'י, גם לזה הם היו הרי מוצאים תירוצים.

למשל האופצייה השנייה (מילוי בעזרת האות י') עושה שימוש באות הראשונה של השם הקדוש "יהוה", אז ברור שזו הבחירה הנכונה... וגם מילוי ה' (האופצייה השלישית) הוא קיצור שמו הקדוש של אלוהים, אז גם זו הבחירה הכי הגיונית...

נ.ב - לדברי יוצר הסרטון התגלית היא של הרב יצחק גינזבורג, ומופיעה גם בספריו של הרב שמואל יניב "צפונות בתורה".

באמת נחמד להציג בצורה סלקטיבית מילים שיוצרות את סדרת פיבונאצ'י, ולטעון שזה פלא גדול. אך מה לגבי כל המילים החשובות ובעלות המשמעות, שלא יוצרות את סידרת פיבונאצ'י?

הנה רשימה של מילים וביטויים מאוד חשובים ביהדות:

"יהוה", "אלוהים", "אלהים", "תורה", "יהוה אמת", "אלוהים אמת", "בראשית", "טוב", "ישראל"...

כל אלה אינם מייצרים את סדרת פיבונאצ'י, למרות שדווקא בהם היינו מצפים שהסדרה תיווצר, למה לזה אין התייחסות?

מצאתם כמה מילים שיוצרות את סדרת פיבונאצ'י, ואז אתם מתרצים בדיעבד כל מקרה ומסבירים מדוע הכי הגיוני שדווקא המילה הזו תייצר את הסדרה?

הרי גם אם המילים "יהוה", "תורה", או "אלוהים אמת" היו יוצרות את סדרת פיבונאצ'י (והן לא) הייתם מספרים לנו בהתלהבות (ועם מוזיקה דרמטית) מדוע זה הכי הגיוני בעולם שדווקא בהן הסדרה תיווצר.

שאלה:

מדוע המילים והאותיות מייצרות את סדרת פיבונאצ'י רק במקומות הזוגיים, או האי-זוגיים? אלוהים, עם כל היכולות שלו, לא יכל לסדר אותיות ומילים שיוצרות את סדרת פיבונאצ'י המלאה? לא רק חצי? ובלי חורים באמצע?

נקודה למחשבה:

א', ה', ל', פ', ארבעת האותיות היחידות באלפבית העברי שמייצרות (לבדן, ללא תוספות) את סדרת פיבונאצ'י, מאפשרות להרכיב גם את הביטויים הבאים:

האל לא פה!

אל? לא לא לא!

הביטוי "פלאפל אמת", יוצר גם הוא את סדרת פיבונאצ'י.

מה יש לכם לומר על זה, חכמולוגים?

גם הביטוי הבא:

הא האא!

אשר מייצג צחוק פרוע, מייצר את סדרת פיבונאצ'י.

ואם זה לא מספיק, אז גם באלפבית ההולנדי, הביטוי:

!Ha hah

המייצג גם הוא צחוק פרוע, מייצר את סדרת פיבונא'צי בכל המיקומים האי-זוגיים!

מעניין הא?

אולי הדבר בא לרמוז לנו, שכל הצפנים המטופשים האלה הם לא יותר מבדיחה וליצנות, ואין צורך להתייחס אליהם ברצינות מעבר לאפקט הבידורי שבעניין.

תשובה:

אין דין הגרלה אקראית של מחשב, לבחירה מכוונת של אדם!

לא ניתן להשוות הגרלה אקראית של מחשב, לבחירה מודעת של אדם, שיכול לכוון את הדברים (במודע, או שלא במודע) לתוצאה שאליה הוא שואף להגיע. בעיקר כשהוא כה להוט להראות לכולם שהאמת בצד שלו...

חישבו על ארגז גדול, המלא בכדורים צבעוניים, שעל כל אחד מהם כתובה ספרה אקראית שערכה הוא בין 0 ל 9. ואז המחזיר בתשובה שולף מהארגז 10 כדורים בזה אחר זה, וזה ערכם לפי סדר הוצאתם מהארגז:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

המחזיר בתשובה מסתכל על התוצאה, ומכריז: "זה נס! מה הסיכוי שאשלוף עשרה כדורים מהארגז, וכבר בניסיון הראשון תצא לי סדרה מסודרת כזו?!".

ואכן, מבחינה סטטיסטית הסיכוי שתתקבל סדרה מסודרת כזו באקראי הוא סיכוי של 1 ל 10 מיליארד, דיי שואף לאפס...

אבל

וזה אבל גדול מאוד... כאשר המחזיר בתשובה הוציא את הכדורים מתוך הארגז, הוא לאו דווקא שלף אותם באופן אקראי. הוא יכל לבחור באופן מכוון את הכדורים שיתנו לו את הסדרה שהוא רוצה, שהרי הוא ראה אותם לנגד עיניו...

עוד מעט נראה, שגם ב"ספרות הקודש" היהודית, ישנם איותים שונים עבור האותיות, וכל אדם בעל ידע מתמטי בסיסי, יכול לבחור באופן מכוון את האיות "הנכון" שמייצר את סדרת פיבונאצ'י... בדומה לבחירת הכדורים מהארגז.

כפי שהוסבר קודם, לא ניתן להשוות בחירה אקראית של מחשב, לבחירה מכוונת ומודעת של אדם, בעיקר כזה שכל כך להוט להראות שהוא צודק...

אבל רגע, למה ללכת רחוק?

סימולציות, סטטיסטיקה, בדיקות...

אותה תופעה בדיוק מתרחשת גם באלפבית ההולנדי!

ושם, לא רק 4 אותיות מייצרות את סדרת פיבונאצ'י, אלא 15 אותיות!

יותר ממחצית האותיות באלפבית ההולנדי מייצרות אותה !!

יחי המלך החדש!

כנראה שהולנדית היא שפת הקודש האמיתית!

זהו האלפבית ההולנדי.

כל אחת מהאותיות המודגשות יוצרת את סדרת פיבונאצ'י במיקום זוגי או אי-זוגי.

כמו בעברית, גם לאלפבית ההולנדי יש מספר גרסאות, שכל אחת שונה מעט באיות שלה. האלפבית שמוצג כאן הוא אחד הנפוצים ביותר, ומופיע באתרי אינטרנט וסרטונים ללימוד השפה ההולנדית.

זהו בסך הכל האלפבית (הלא עברי) השני שנבדק. האלפבית שנבדק לפניו, היה גם הוא אלפבית הולנדי (עם איות מעט שונה) ושם התקבלו 4 אותיות שמייצרות את סדרת פיבונאצ'י...

אתם עדיין חושבים שמדובר על תופעה נדירה שייחודית רק לעברית?

זהו האלפבית הגרמני (דומה מאוד להולנדי).

גם כאן נוצרת סדרת פיבונאצ'י בשתי האותיות המסומנות (A ו H), שאר האותיות לא נבדקו, ייתכן מאוד שישנן אותיות נוספות שיוצרות את הסדרה.

ולמה דווקא סדרת פיבונאצ'י?

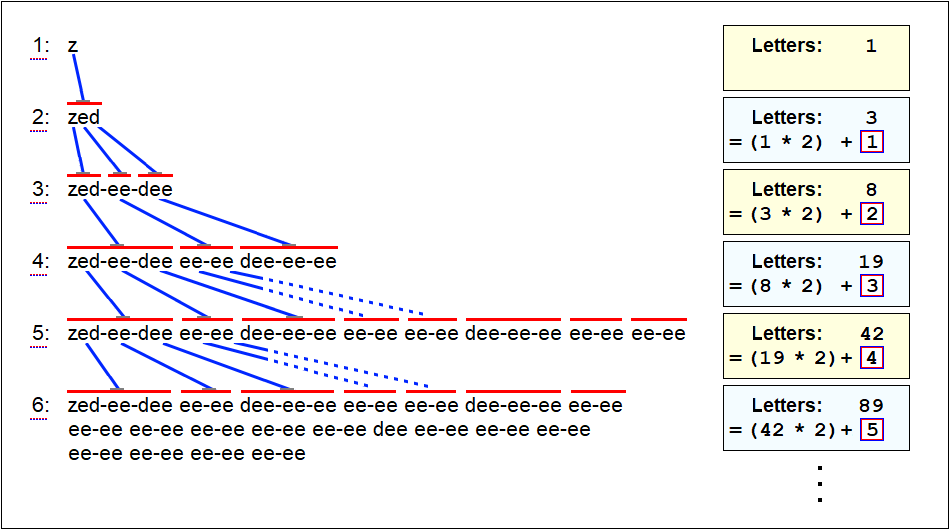
גם האלפבית האנגלי מייצר לנו סדרה נחמדה.

כפי שאפשר לראות באיור המושקע, אם נתחיל לפרט את האיות של האות Z (האות האחרונה באלפבית האנגלי) על פי אותם כללים שראינו קודם, נקבל סדרה מעניינת שבה מספר האותיות בכל שלב, שווה למספר האותיות בשלב הקודם כפול 2, פלוס ערך שגדל ב 1 בכל שלב (1, 2, 3, 4, 5...).

ערך זה מודגש באיור בריבוע אדום כחלחל.

למה הסדרה מתקבלת דווקא באות האחרונה של האלפבית?

קודם כל, האות נבחרה לגמרי באקראי עבור הבדיקה, וייתכן מאוד שישנן אותיות נוספות באלפבית האנגלי שמייצרות סדרות מעניינות.

דבר שני, למה לא?

אתם חושבים שאם האות האחרונה באלפבית העברי (האות ת') הייתה מייצרת את סדרת פיבונאצ'י, יוצר הסרטון לא היה מציג זאת כ-נס קפה גדול?

הוא בטח היה מסביר שזה מאוד הגיוני, כי זו האות הראשונה במילה "תורה", שזה הדבר הכי חשוב שאלוהים נתן לעם ישראל... וכמו כן האות האחרונה מייצגת גם את הדבר השלם, מא' עד ת'...

אז הנה, יש צידוק להשתמש גם באות האחרונה, והרי גם חז"ל אמרו:

אחרון חביב - לתל אביב.

(הם לא באמת אמרו את זה)

אז מה הטריק פה?

כמו בכל "הצפנים" שהמחזירים בתשובה אוהבים להתהדר בהם, גם כאן הטריק המרכזי הוא מרחב משחק גדול מספיק שמאפשר לשחק עם הפרמטרים, "לתפור" מהם את התוצאה הרצוייה, ואז לתרץ בדיעבד מדוע דווקא זו הייתה הבחירה הכי נכונה והכי הגיונית...

או כמו בהרבה צפנים אחרים, פשוט לא לספר לקהל שמקשיב שהיו עוד אלטרנטיבות, ושזו רק אחת מהן שנבחרה בקפידה רבה, כדי לתת למחזיר בתשובה את מה שהוא מראש רצה להראות...

טריק נוסף בצופן הנוכחי, הוא ידע מתמטי קצת מעבר לממוצע. ידע המאפשר למחזיר בתשובה לבצע בחירה אופטימלית של האיות הספציפי שייתן את סדרת פיבונאצ'י, ואז להציג זאת כקסם מדהים, או נס גדול משמים.

הטריק

הטריק המתמטי כאן דיי פשוט. כל מה שצריך כדי לייצר את סדרת פיבונאצ'י, זה אלפבית שמכיל בתוכו שני סוגי אותיות:

אות מסוג 1:

אות שהשם שלה מורכב משלוש אותיות: שתיים מסוג 1, ואחת מסוג 2.

למשל 'H' באלפבית ההולנדי, שמאוייתת: Hah.

אות מסוג 2:

אות שהשם שלה מורכב משתי אותיות: אחת מסוג 1, והשנייה מסוג 2.

למשל 'A' באלפבית ההולנדי, שמאוייתת: Ah.

וזהו! בכל אלפבית כזה מובטח שתיווצר סדרת פיבונאצ'י!

(בכל אות שהיא מסוג 1 או 2)

כל אות מסוג 1 תיצור את סדרת פיבונאצ'י במיקומים האי-זוגיים, וכל אות מסוג 2 תיצור את הסדרה במיקומים הזוגיים.

(קרדיט לגדי אלקסנדרוביץ' מהבלוג המתמטי "לא מדויק")

ברגע שמבינים את העיקרון הפשוט הזה, קל לשחק עם האיותים השונים, ולתפור מהם קומבינציה שתייצר את סדרת פיבונאצ'י:

לוקחים אלפבית, ובודקים אם הוא מכיל אותיות שיוצרות, או מתחילות ליצור את סדרת פיבונאצ'י.

(אפשר לבדוק בקלות באמצעות תוכנת מחשב, ואפשר גם לבדוק ידנית על גבי דף נייר - לפחות את השלבים הראשונים. כך למשל נמצאה הסדרה שראינו קודם באלפבית האנגלי).

אם האלפבית לא יוצר את סדרת פיבונאצ'י, משחקים קצת עם סוגי איות שונים (ויש הרבה שאפשר לבחור מהם) עד שמגיעים לתוצאה הרצוייה.

והופ!

יש "נס" שאפשר לנפנף בו מול קהל הפתיים שבולע את ההבלים האלה.

ואז ממציאים תירוצים בדיעבד, מדוע הכי הגיוני להשתמש דווקא באיות הזה, ומדוע דווקא המילים והאותיות שמוצגות בסרטון יוצרות את סדרת פיבונאצ'י, תוך התעלמות מהמון אותיות ומילים אחרות (כמו למשל: "יהוה", "תורה", "אלוהים") שלא מייצרות את הסדרה.

כמו תשבץ סודוקו, משחקים קצת עם המספרים, עד שמגיעים לפיתרון.

טריק קוסמים

הדבר דומה לקסם מדהים שאנו רואים במופע קסמים, ואיננו מבינים כיצד הוא נעשה. האם זה שאיננו מבינים את הטריק שעומד בבסיס הקסם, אומר שהקוסם ביצע אותו באמצעות כוחות על טבעיים? או כישוף?

רובנו מבינים הרי כאנשים בוגרים, שקסמים שקוסם מציג על הבמה, למרות שהם נראים מדהימים, ולמרות שנראה כאלה הם סותרים כביכול את חוקי הטבע, מבוססים בעצם על טריקים פשוטים ועל אחיזת עיניים.

אז מדוע כשרבנים ומחזירים בתשובה מציגים לפנינו "צפנים" שנראים כמו קסם, אנו ממהרים לקבל את טענותיהם, במקום לבחון את הדברים לעומק?

אפליקציה לבחינת הנושא:

אם מישהו מעוניין להשתעשע עם הנושא, ניתן ניתן להוריד כאן את התוכנה שבאמצעותה התגלו הממצאים שפורטו קודם.

בניגוד לתוכנה שיוצר הסרטון השתמש בה, שלצורך הספירה צוברת את האותיות בבאפרים ענקיים (מערכים) אשר גדלים בכל מחזור באופן מעריכי (אקספוננציאלי) וגורמים למחשב לקרוס בשלב מסויים (מפני שהמקום בזיכרון פשוט נגמר), הקוד שנעשה בו שימוש כאן, מבצע את הספירה בזמן אמת (On-the-fly) ללא כל אגירה של האותיות בזיכרון.

ישנן שתי גרסאות לאפליקציה, אחת עבור האלפבית העברי (עם איות כפי שמוצג בסרטון), וגרסה נוספת עבור האלפבית ההולנדי.

להלן צילומי מסך של האפליקציה:

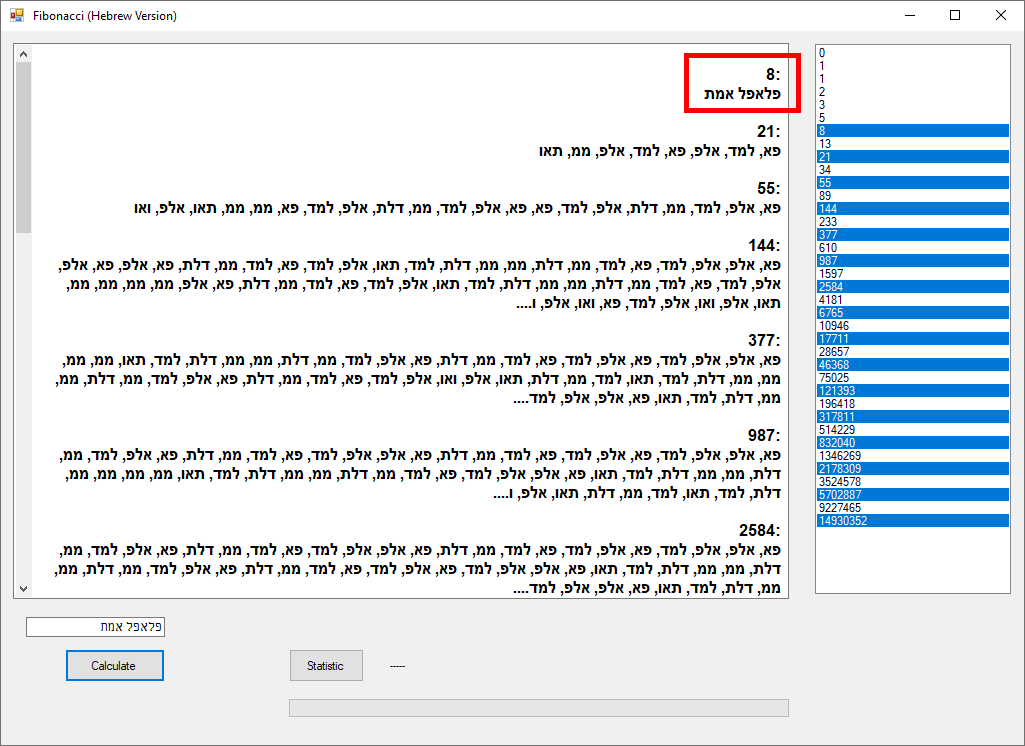
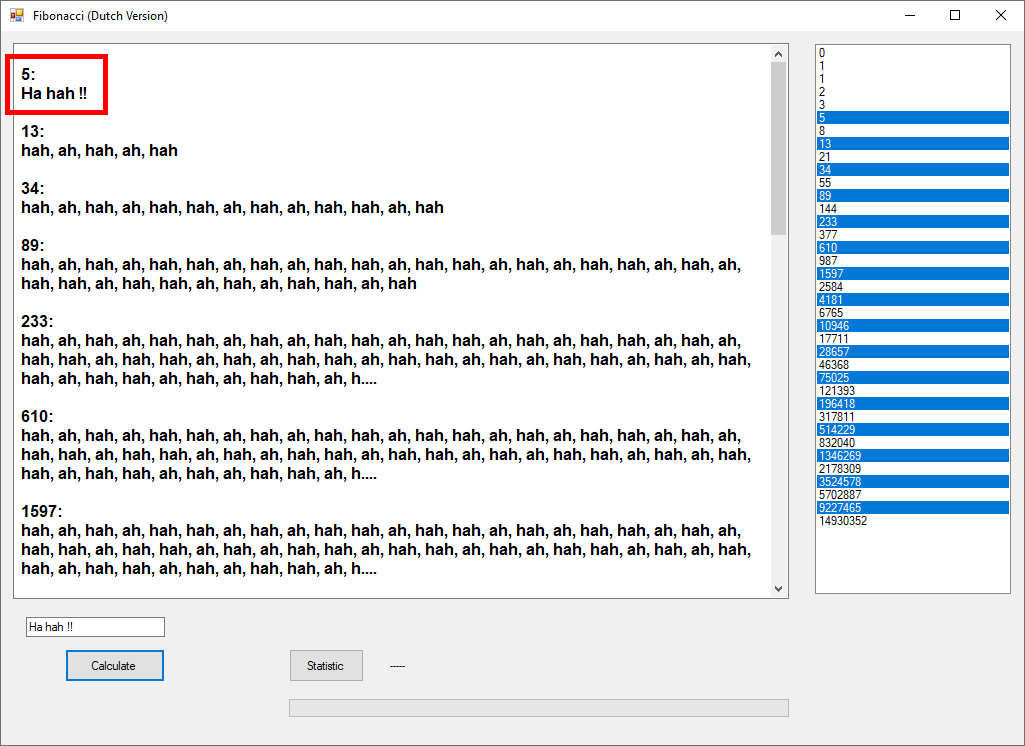
בדיקה מהירה בספריות ומאגרי ספרי קודש רבניים שיוצר הסרטון בעצמו הפנה אליהם, מעלה מהר מאוד דוגמאות רבות לסוגי איות אחרים שאינם תואמים לאיות שמוצג בסרטון (האיות שיוצר את סדרת פיבונאצ'י).

מה שמראה שהיה כאן מרחב תמרון גדול מאוד, שאיפשר לשחק עם סוגי איות שונים, ולתפור מהם את האיות הספציפי שייתן את סדרת פיבונאצ'י.

הדוגמא הראשונה ("אורחות חיים") לקוחה מתוך דף ספציפי שיוצר הסרטון בעצמו נתן כדוגמא לשימוש באיות שמוצג בסרטון בספרי הקודש!

הוא אפילו לא שם לב, שאחת האותיות בדף (האות מ') מאוייתת בצורה שונה מהאיות שמופיע בסרטון... בדיקה מהירה בעזרת תוכנה שנכתבה במיוחד לצורך העניין, מראה כי איות כזה לא מייצר את סדרת פיבונאצ'י...

דוגמאות נוספות

על מנת שלא להעמיס על הדף, הדוגמות שמוצגות כאן הן רק תמצית של האיותים הסותרים שנמצאו, כאלו שאינם תואמים לאיות שמוצג בסרטון.

ריכוז מפורט יותר של דוגמאות אפשר לראות כאן.

נתחיל בזה שלא בטוח בכלל שסדרת פיבונאצ'י באמת מופיעה בכל המקומות שמייחסים לה... לעיתים נדמה שהיא מופיעה במקום מסויים, אך בדיקה קפדנית ומעמיקה יותר מראה שזה רק למראית עין.

ישנן המון תופעות ספירליות בטבע:

צורתן של קונכיות רבות, סופות הוריקן, גלקסיות ספירליות, ואפילו המים שמסתחררים לנו באמבטיה מעל פתח הניקוז כאשר פותחים את הפקק.

כל צורה לוליינית או ספירלית כזו מיד עושה לאנשים אסוציאציה לסדרת פיבונאצ'י, אז הם מניחים באופן אוטומטי כי מדובר על אותה תופעה.

אך כשבוחנים את הדברים לעומק, מגלים שלעיתים רבות זה רק נראה דומה...

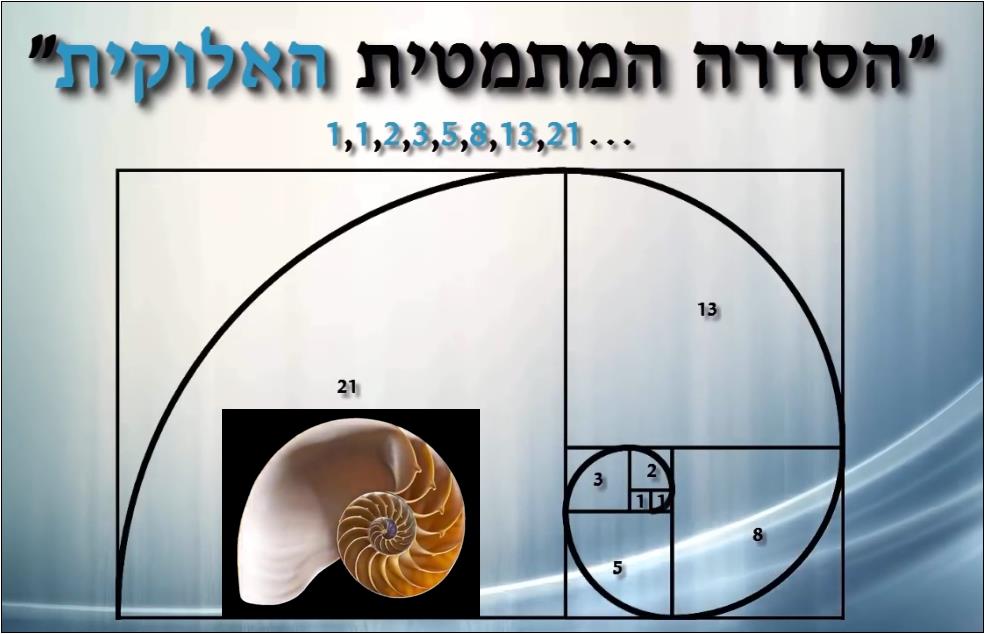
הסבר קצר לגבי האיור

בתמונה (צילומי מסך מתוך הסרטון) מוצגת ספירלת פיבונא'צי.

מתחילים עם ריבוע שאורך כל צלע בו היא 1, ואז מתחילים לצרף ריבועים נוספים מסביב (במסלול מעגלי, נגד כיוון השעון) שהצלע של כל אחד מהם שווה בגודלה לצלעות של הריבועים שצמודים אליה.

כפי שאפשר לראות בתמונה, מה שמקבלים זו סדרה של ריבועים, שגודלם זהה לאיברים בסדרת פיבונאצ'י: 1, 1, 2, 3, 5, 8, 13, 21....

אם נבדוק את היחס בין צלעו של כל ריבוע באיור, לצלע של הריבוע שצוייר לפניו, נגלה כי אנחנו הולכים ומתקרבים (ככל שהריבועים גדלים) לערך 1.618033, המכונה "יחס הזהב", אשר יש לו שימושים חשובים במתמטיקה.

למשל, אורך צלע בריבוע הגדול ביותר באיור הוא 21, ואורך צלעו של הריבוע שצמוד אליו (וצוייר לפניו) הוא 13.

אם נחלק 21 ב 13 נקבל 1.615384.

ואם נמשיך להוסיף ריבועים נוספים, ונבדוק את היחס ביניהם, נראה שהערך הולך ומתקרב יותר ויותר ליחס הזהב, שהוא מספר בעל אינסוף ספרות.

כמו כן, אם נשרטט קו מעוקל רציף שעובר דרך פינותיהם של הריבועים, נקבל ספירלה, שהיא הספירלה המפורסמת של סדרת פיבונאצ'י, זו שמייחסים לה תופעות טבע רבות.

בדיקה מעמיקה יותר

ניסיונות להגיע להתאמה בין הספירלה של סדרת פיבונאצ'י, לספירלה של קונכיות המוצגות באתרים רבות כקשורות לסדרה זו, נכשלו בזה אחר זה.

לא משנה כמה מנסים לשחק עם הגודל והזווית (כמובן תוך שמירה על אותן פרופורציות של רוחב וגובה) הספירלות פשוט לא תואמות זו לזו.

מגיעים להתאמה בחלק אחד, ואז חלק אחר בורח לגמרי החוצה...

חיפוש מהיר באינטרנט, מעלה מהר מאוד מאמרים (חלקם פורסמו ע"י מתמטיקאים במגזינים מדעיים) שמדברים בדיוק על זה, על כך שמדובר פשוט במיתוס.

הנה כמה ציטוטים חלקיים מתוך אותם מאמרים -

(תרגום מאנגלית לעברית)

"עבדתי על הרצאה קצרה בנושא סדרת פיבונאצ'י עבור שיעור מתמטיקה של חבר, חיפשתי תמונה של קונכיית נאוטילוס שאוכל להלביש עליה את הספירלה של סדרת פיבונאצ'י... אבל פשוט לא הצלחתי לגרום להן להתאים!"

"לא משנה כמה ואיך הגדלתי או הקטנתי את הספירלה, היא פשוט לא התרחבה באותו קצב כמו קונכיית הנאוטילוס. פניתי לגוגל תמונות, וניסיתי מספר תמונות שונות של קונכיות נאוטילוס, וקיבלתי את אותה תוצאה בדיוק... פשוט לא הצלחתי לגרום לספירלות להתאים זו לזו"

"מאמר של חדשות המדע שכותרתו "צדפות ים ספירליות" הראה שאני לא היחיד, בשנת 1999, המתמטיקאי בדימוס קלמנט פלבו מדד סדרה של קונכיות נאוטילוס באקדמיה למדעים בקליפורניה בסן פרנסיסקו, וגילה שאמנם הן היו ספירלות לוגריתמיות (כמו ספירלת הזהב), אך היחס שלהן (שנע בין 1.24 ל-1.43 לערך) אפילו לא קרוב ליחס של 1.618 שקיים בספירלת הזהב"

"בשנת 2002, ג'ון שארפ הבחין באותה בעיה, אך אף על פי כן, במקומות רבים עדיין מתעקשים שחתך הרוחב של קונכיית נאוטילוס מציג דפוס צמיחה של יחס הזהב..."

"נסו לחפש בגוגל: פיבונאצ'י נאוטילוס, ותקבלו ים של דפים המציגים קונכיה זו כהמחשה לספירלת פיבונאצ'י (או יחס הזהב) בטבע... במשך עשרות שנים קראתי בספרים ובמגזינים על נאוטילוס כדוגמא לסדרת פיבונאצ'י"

"הכותבים פשוט מעבירים את מה שהם קראו במקומות אחרים... בדיוק כפי שאני עשיתי במשך כל השנים האלו. אף אחד מהם לא ממש מדד מעולם קונכיית נאוטילוס ובדק אם באמת יש התאמה"

"לשמחתי, זה בעצם עשוי להיות נושא אפילו טוב יותר להרצאה שלי מאשר איור הנאוטילוס שתכננתי במקור:

אל תאמין לכל מה שאתה קורא.

זהו שיעור טוב לתיכוניסטים, ורלוונטי גם עבורנו המבוגרים..."

"לעתים קרובות מדי, אנו לוקחים את מה שאנו שומעים בתור עובדה. אך מסתבר שהרבה פעמים "עובדות" שמוצגות לנו, אינן באמת עובדות, כמו המיתוס המפורסם על כך שאנו משתמשים כביכול רק ב 10% מהמוח שלנו..."

"קחו למשל את סדרת פיבונאצ'י, נאמר לנו שתבנית המספרים המעניינת הזו מופיעה בהרבה תופעות טבע, כולל דפוסי הספירלה שאנו רואים בכל מקום. החל מקונכיות לוליניות ועד לגלקסיות ספירליות. הבעיה היא שהתבוננות מעמיקה לא תומכת בטענות אלו"

"הסתכלו למשל, על צורתה של קונכיית וולק. אומרים לנו שבמבט צד, מופיעה בה סדרת פיבונאצ'י, אבל זה לא באמת נכון. כשמסתכלים על הספירלות, מגלים שהן שונות בתכלית"

"הספירלה המתמטית של סדרת פיבונאצ'י נפתחת הרבה יותר מהר. לקונכיה יש ספירלה הדוקה יותר - הספירלה של קונכיית וולק עושה בערך שני סיבובים על כל סיבוב של ספירלת פיבונאצ'י"

"האם הספירלה של קונכיית נאוטילוס באמת תואמת לסדרת פיבונאצ'י? בגיליון הנוכחי של המגזין האקדמי המתמטי, המתמטיקאי בדימוס קלמנט פלבו טוען כי למעטפת הנאוטילוס אין באמת צורת ספירלה התואמת ליחס הזהב"

"כאשר פלבו מדד קונכיות נאוטילוס באוסף שנמצא באקדמיה למדעים של קליפורניה בסן פרנסיסקו, הוא גילה שהיחסים הנמדדים נעו בין 1.24 ל-1.43"

"זה נראה מאוד לא סביר שקיימת קונכיית נאוטילוס שמתקרבת ליחס הזהב, וגם אם תימצא כזו אני חושב שהיא תהיה נדירה ולא טיפוסית, מסכם פלבו"

"במאמר משנת 2002 במגזין המקוון נטוורק נקסוס (ארכיטקטורה ומתמטיקה אונליין) ג'ון שארפ הצביע על אותה בעיה. מדידותיו על קונכיות נאוטילוס אישרו גם הן, כי הספירלה של יחס הזהב וספירלת הנאוטילוס פשוט אינן תואמות"

"ואף על פי כן, אנשים רבים עדיין מתעקשים שחתך הרוחב של קונכיית נאוטילוס מציג דפוס צמיחה שתואם לסדרת פיבונאצ'י (יחס הזהב). אנשים מניחים אוטומטית שמכיוון שניתן להשתמש ביחס הזהב כדי לצייר ספירלה לוגריתמית, אז כל הספירלות של קונכיות קשורות ליחס הזהב, כשלמעשה הדבר אינו נכון"

"אחד הדברים המדהימים בתפיסות שגויות אלו הוא שהן כל כך נפוצות, אפילו בקרב מתמטיקאים שאמורים לדעת טוב יותר. זוהי דוגמה מובהקת מדוע יש ללמד גיאומטריה בצורה רחבה יותר, ולא רק גיאומטריה, אלא גם הערכה חזותית של צורות ופרופורציות"

"וכדאי תמיד גם לבדוק את הדברים בעולם האמיתי, מציין שארפ"

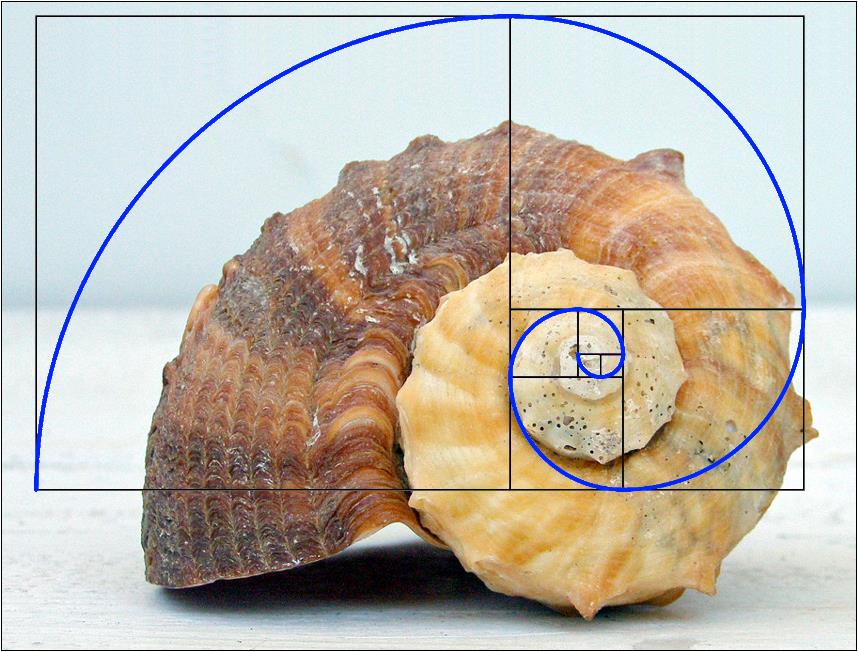
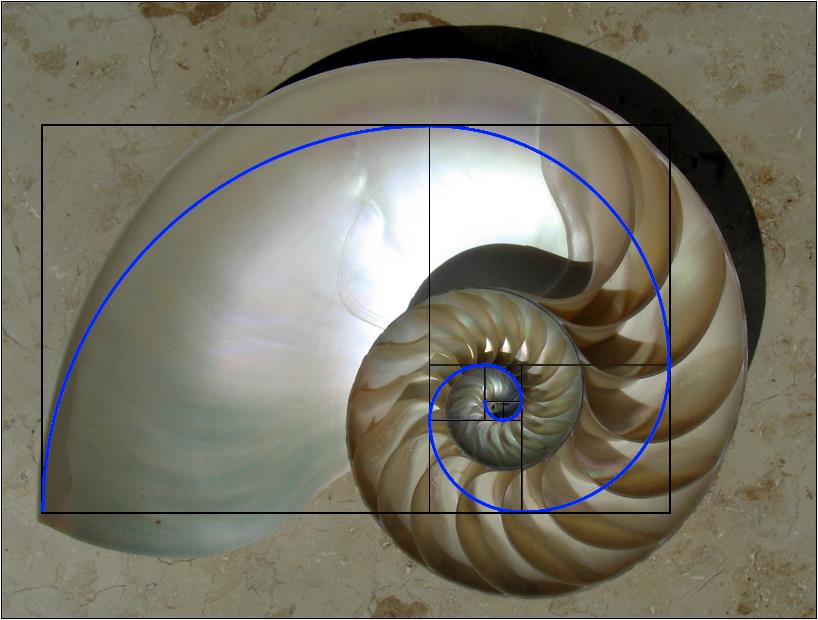
אלו שתי דוגמאות מתוך ניסיונות רבים שנעשו להתאים את הספירלה של סדרת פיבונאצ'י לספירלה של קונכיות.

גם ניסיון להתאים את הספירלה החיצונית של הקונכייה לספירלה של סדרת פיבונאצ'י נכשל, ומהר מאוד הספירלות הפנימיות נפרדות זו מזו לשלום...

מה רואים כאן?

דרך יעילה ומדוייקת יותר לבדוק התאמה לספירלה של סדרת פיבונאצ'י, היא לבדוק מה היחס בין שני מלבנים צמודים העוטפים את הספירלה.

אם זו ספירלה של סדרת פיבונאצ'י, הערך שמתקבל צריך להיות 1.618, שהוא יחס הזהב. אך כפי שניתן לראות, הערך שמתקבל רחוק מאוד מערך זה...

בקונכיות נבדקו גם הספירלות הפנימיות, ובתמונת הגלקסיה (צילום מפורסם של נאס"א) נבדקו גם הזרועות החיצוניות, אך אין שום התאמה ליחס הזהב.

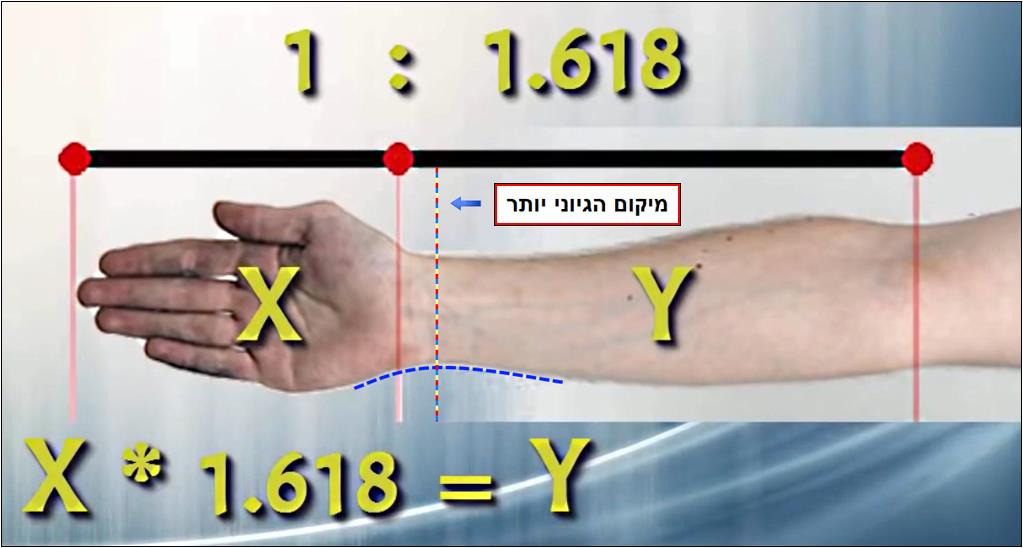
דוגמא נוספת ואחרונה (ואין שום כוונה לבדוק כל דוגמא וכל נתון שמוצגים בסרטון זה או בסרטונים האחרים, אלא רק להראות כמה דוגמאות מייצגות).

כמה נוח לסמן את תחילת כף היד בדיוק במיקום שנותן את יחס הזהב 1.618... אך האם הקביעה הזו באמת אובייקטיבית? תנו לעשרה אנשים לסמן היכן לדעתם מתחילה כף היד, ותקבלו 10 תשובות שונות...

אין באמת מיקום ספציפי שניתן לומר עליו "כאן מתחילה כף היד". ישנו מעבר הדרגתי בין הזרוע לכף היד, ולכן מדובר על קביעה שנתונה לפרשנות.

אם כבר רוצים להיות אובייקטיביים, אז הרבה יותר הגיוני לסמן את תחילת כף היד במקום שבו הזרוע מתחילה להתרחב, כפי שמודגש בעזרת הסימון הכחול המקווקו באיור, ובקו המקווקו האנכי שחוצה אותו.

אם קובעים שם את נקודת המעבר בין הזרוע לכף היד, היחס יוצא:

1.3164

רחוק מאוד מיחס הזהב ומסדרת פיבונאצ'י....

זה לא מה שנאמר.

ייתכן שהסדרה קיימת בטבע, אך בוודאי שלא בכל המקומות שמיוחסים לה.

כפי שצויין קודם, ישנן המון תופעות ספירליות בטבע, כך שהגיוני, אפילו מתוך מקריות גמורה, שחלקן תואמות לסדרת פיבונאצ'י, לפחות בצורה מקורבת.

כמו כן, אנו יודעים שתופעות רבות בטבע נוצרות כתוצאה מאיזון בין כוחות פיזיקליים, והגעה למצב של שיווי משקל ויעילות אנרגטית אופטימלית.

זו למשל הסיבה שבגללה טיפת מים נוטה להיות עגולה (ולא משולשת, או עם קצוות חדים), זו הסיבה לכך שהאבולוציה דחפה את הדבורים לבנות את תאי הדבש בכוורת בצורת משושים, ולא בצורה עגולה או מרובעת, וזו הסיבה לכך שרוב כוכבי הלכת סובבים סביב השמש שלהם על אותו מישור, ולא כל אחד בזווית אחרת.

(ומי שרוצה מוזמן להרחיב בנושא באמצעות חיפוש באינטרנט)

ייתכן שגם לצורה לוליינית (ספירלית) התואמת את סדרת פיבונאצ'י, יש יתרון כלשהו מבחינת יעילות אנרגטית, ואיזון בין כוחות פיזיקליים.

אולי זה מה שדחף מערכות מסויימות בטבע ליצור ספירלה שתואמת במידה מסויימת לספירלה של סדרת פיבונאצ'י.

לכן אין צורך לקפוץ למסקנות מרחיקות לכת, ולהניח כי מדובר בתכנון תבוני.